Diffusion Notes

Overview

Diffusion models are generative models which have most recently gained notoriety being used in OpenAI’s DALL-E 2 and Stable Diffusion. Diffusion works by destroying training data by first successively adding Gaussian noise to an image, and learning to recover the data by reversing the noise process.

Forward Diffusion

Given a data point sampled from a real distribution $x_0 \sim q(x)$, we define a foward diffusion process in which we add small amounts of Gaussian noise to our given data point in $T$ steps, which produces a series of noisy samples $x_1, \dots, x_T$, of which $x_T$ is equivalent to an isotropic Gaussian distribution. The step sizes are controlled by a variance schedule ${\{ \beta \in (0,1) \}}^T_{t=1}$. We model the current $x_t$ based on $x_{t-1}$ which we can model as a markov chain (where each step only depends on the step before it) as follows:

\[q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1- \beta_{t}x_{t-1}} \beta_{t}I)\]

where the $\mathcal{N}$ represents the normal distribution, the first term $x_t$ represents the output, the second term $\sqrt{1- \beta_{t}x_{t-1}} \beta_{t}$ represents the mean, and the third term $\beta_{t}I$ represents the variance. $\beta$ refers to the scheduler since we don’t apply the same amount of noise during each timestep.

This statement can be equivalently written as \(X_t = X_{t-1} = \mathcal{N}(0,1)\)

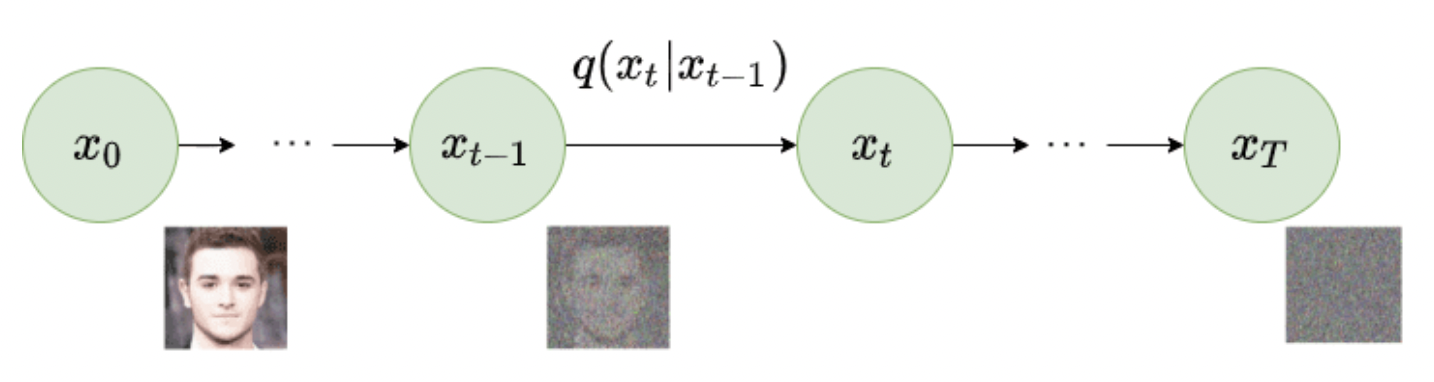
The downside of this diffusion technique is that we have to it $T$ iterations. To sidestep this we use the reparameterization trick, we can rewrite the formulation such that we can get our desired sample $x_t$ (without having to compute every iteration from 0:t) as:

\[x_t = q(x_t \bar x_0) = \mathcal{N}({x_t}\sqrt{\bar{a_t}}x_0),(1 - \bar{a}_t)I\]

We define $\alpha_t = 1 - \beta_t$

https://www.assemblyai.com/blog/diffusion-models-for-machine-learning-introduction/

Reverse Diffusion

Notes

https://lilianweng.github.io/posts/2021-07-11-diffusion-models/#ldm https://theaisummer.com/diffusion-models/